11 lavaanGUI für Fortgeschrittene

In den Kapitel 9.2, 9.3 und 9.4 wurde detailliert beschrieben, wie verschiedene Messmodelle der KTT mit Hilfe von lavaanGUI geschätzt und interpretiert werden können. Dabei ist auf die wichtigsten Funktionen der lavaanGUI eingegangen worden, die in den Kapitel 4 und 5 vorgestellt wurden. LavaanGUI kann allerdings noch zu mehr Analysen herangezogen werden. Diese werden in den folgenden Abschnitten dargestellt.

11.1 Vergleich modellimplizierter und empirischer Varianz-Kovarianzmatrix

Die Beurteilung des Modellfits basiert auf dem Vergleich der empirischen Varianz-Kovarianzmatrix mit der modellimplizierten. Die empirische Varianz-Kovarianzmatrix ist dabei die, die entsteht, wenn man die Matrix auf Grundlage der vorliegenden Daten aufstellt. Die modellimplizierte Matrix bezeichnet die, die entsteht, wenn man die Matrix auf Grundlage der vorliegenden Daten und unter Verwendung der Modellannahmen aufstellt. In lavaanGUI kann man sich beide Matrizen anzeigen lassen. Zusätzlich ist es auch möglich die Abweichungen der empirischen von der modellimplizierten Varianz-Kovarianzmatrix anzeigen zu lassen. Der Vorgang ist in drei Schritte gegliedert, die im Folgenden einzeln dargestellt und erklärt werden.

Voraussetzung aller folgenden Beschreibungen und Erklärungen ist es, dass ein Datensatz in lavaanGUI eingelesen worden ist und eine Modellanalyse bereits durchgeführt wurde, also ein Mesmodell über die Syntaxeingabe spezifiziert wurde.

11.1.1 Die modellimplizierte Varianz-Kovarianzmatrix

Um die modellimplizierte Varianz-Kovarianzmatrix in lavaanGUI anzeigen zu lassen, ruft man im Seitenmenü das Untermenü “lavInspect” auf. In dem Untermenü werden zwei Dropdownmenüs angezeigt, “lavInspect Topic” und “What to lavInspect”. Im Dropdownmenü des Topics wählt man “Model implied sample statistics” aus. Damit ruft man die modellimplizierte Varianz-Kovarianzmatrix auf. Zusätzlich muss noch im “What to lavInspect” Menü die Möglichkeit “fittet” ausgewählt werden.

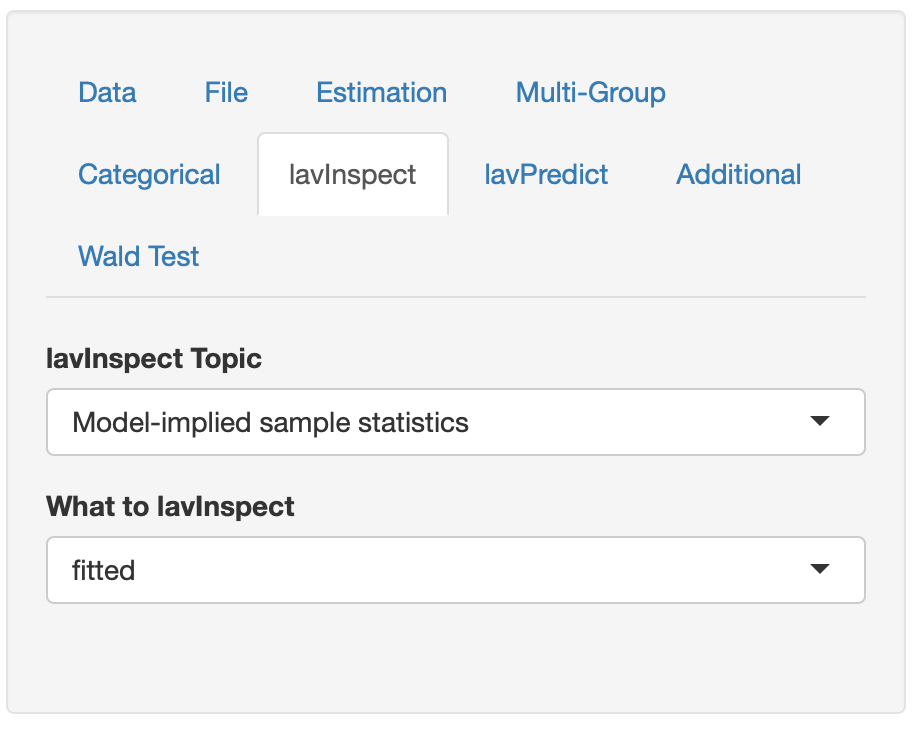
Figure 11.1: Seitenmenü lavInspect - Modellimplizierte Varianz-Kovarianzmatrix

Um sich die Ergebnisse der Berechnung anzeigen zu lassen, muss auch im Hauptmenü das Untermenü “lavInspect” aufgerufen werden. Hierunter wird nun die modellimplizierte Varianz-Kovarianzmatrix sowie die modellimplizierten Mittelwerte angezeigt.

In diesem Beispiel wurde ein $\tau$-paralleles Messmodell spezifiziert. Dafür sieht die modellimplizierte Varianz-Kovarianzmatrix folgendermaßen aus:

Figure 11.2: Hauptmenü lavInspect - Modellimplizierte Varianz-Kovarianzmatrix

11.1.2 Die empirische Varianz-Kovarianzmatrix

Im zweiten Schritt soll die empirische Varianz-Kovarianzmatrix aufgerufen werden. Dazu geht man ähnlich vor, wie auch für die modellimplizierte Varianz-Kovarianzmatrix. Allerdings werden für das Topic und die Schaltfläche “What to lavInspect” andere Menüpunkte ausgewählt. Um die empirische Matrix aufzurufen, wählt man für das lavInspect Topic den Menüpunkt “Observed sample Statistics” und im Dropdownmenü “What to lavInspect” den Menüpunkt “sample Statistics”.

Figure 11.3: Seitenmenü lavInspect - Empirische Varianz-Kovarianzmatrix

Für das $\tau$-parallele Messmodell, was in diesem Beispiel spezifiziert wurde, ist die empirische Varianz-Kovarianzmatrix die Folgende:

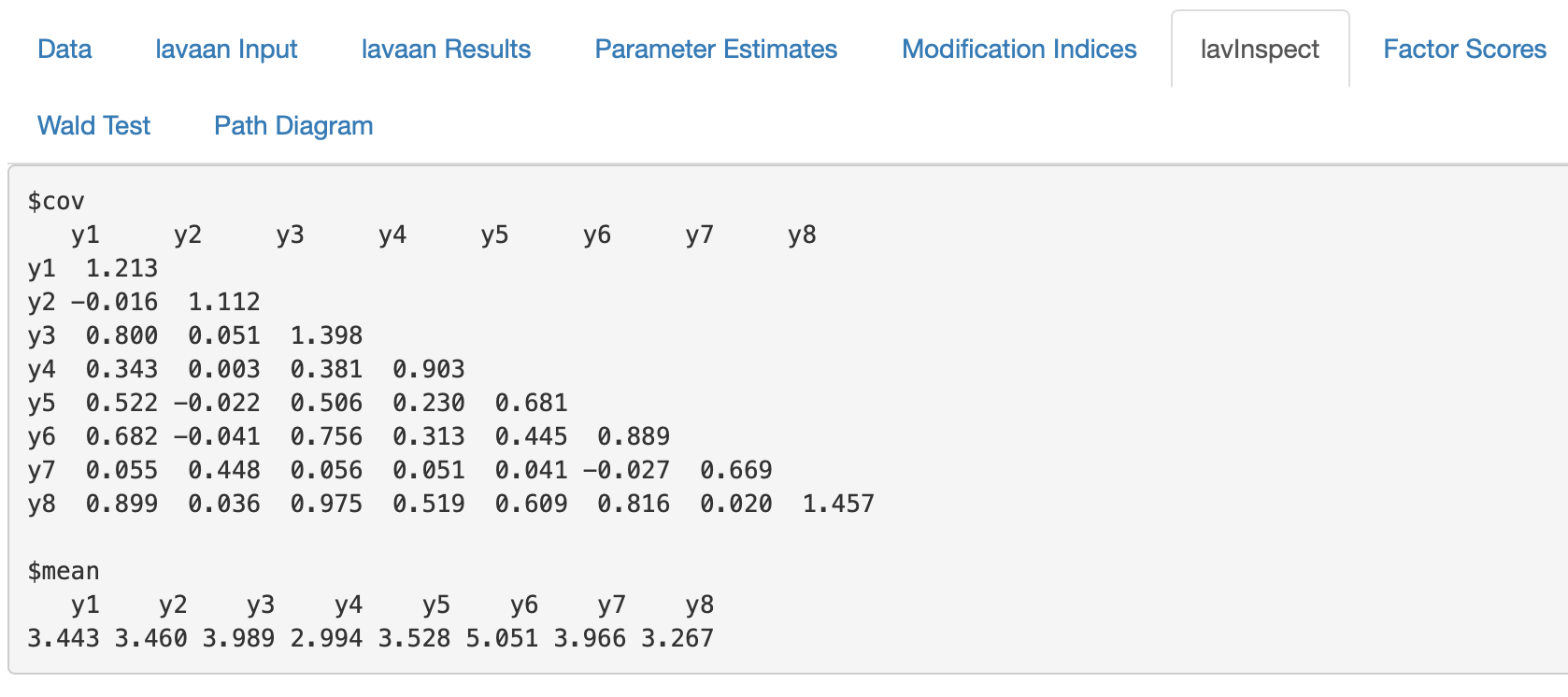
Figure 11.4: Hauptmenü lavInspect - Empirische Varianz-Kovarianzmatrix

Auch hier werden sowohl die Matrix, als auch die Mittelwerte der Variablen dargestellt.

11.1.3 Vergleich modellimplizierte und empirische Varianz-Kovarianzmatrix

Nachdem man beide, die modellimplizierte und die empirische Varianz-Kovarianzmatrix, betrachtet hat, ist es noch von Interesse, inwieweit diese voneinander abweichen. Dazu kann man die Abweichungen der modellimplizierten von der empirischen Varianz-Kovarianzmatrix mit lavaanGUI berechnen und darstellen lassen.Dazu wählt man im Dropdownmenü des Topics den Menüpunkt “All Topics” aus. Im zweiten Dropdownmenü, um zu definieren, was berechnet und dargestellt werden soll, wird der Menüpunkt “residuals” ausgewählt. Damit man im Dropdownmenü nicht alle Untermenüpunkte durchsuchen muss, kann man, sobald man das Dropdownmenü angeklickt hat, beginnen, den Namen des Untermenüpunktes, den man sucht, auf das Tastatur zu schreiben. Daraufhin werden im Dropdownmenü nur noch diese Untermenüpunkte angezeigt, die mit der angeschlagenen Tastaturreihenfolge beginnen.

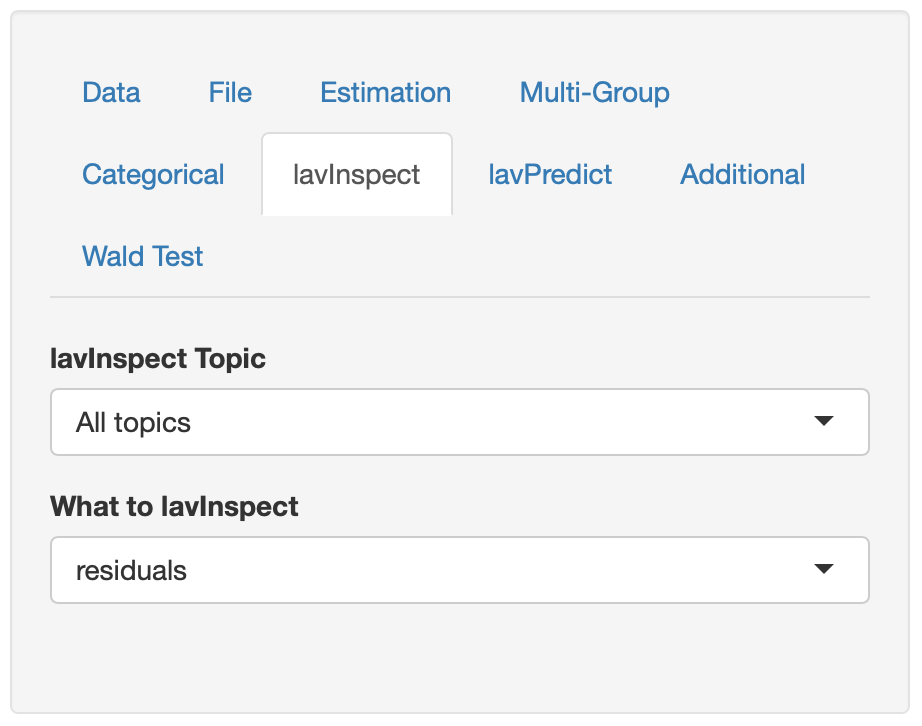
Figure 11.5: Seitenmenü lavInspect - Vergleich der modellimplizierten und der empirischen Varianz-Kovarianzmatrix

Für die oben dargestellte und berechnete modellimplizierte sowie empirische Varianz-Kovarianzmatrix ergiben sich folgende Abweichungen:

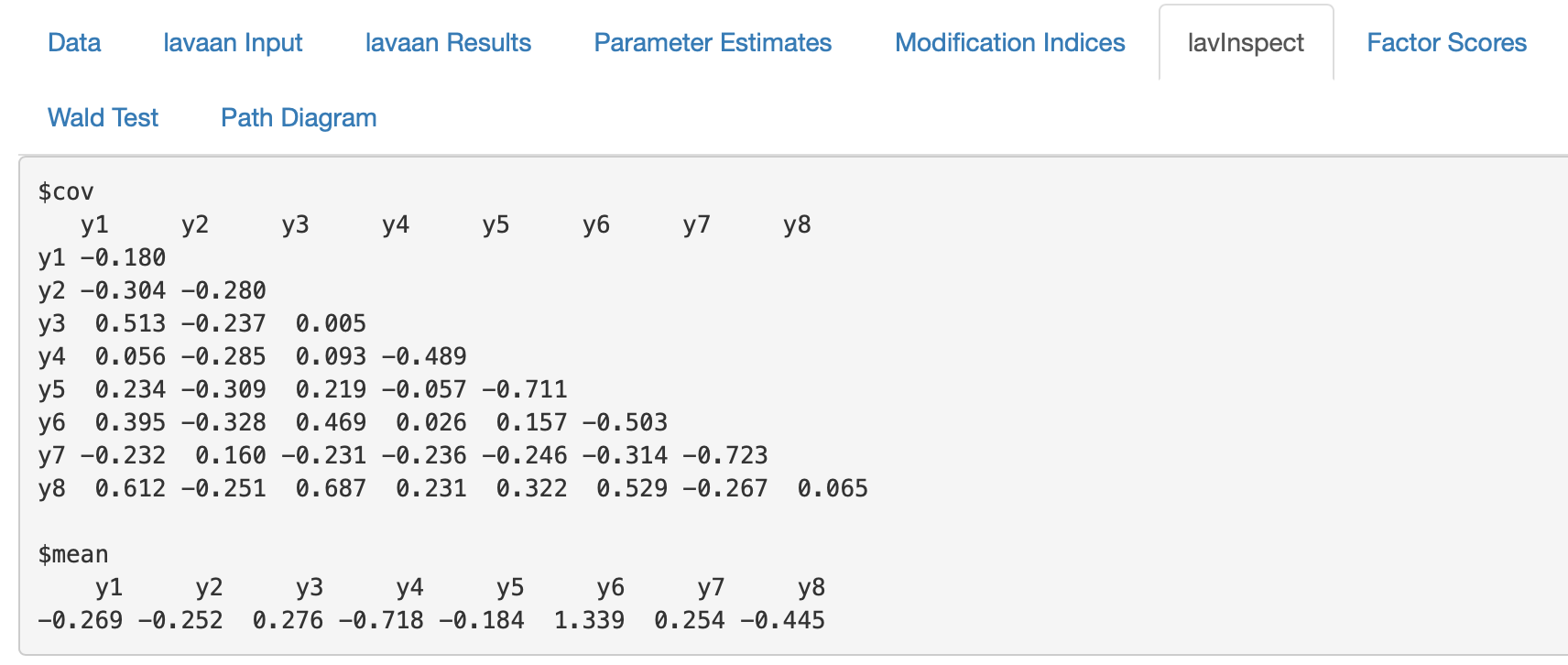
Figure 11.6: Hauptmenü lavInspect - Vergleich der modellimplizierten und der empirischen Varianz-Kovarianzmatrix

Die Abweichungen werden sowohl für die Varianz-Kovarianzmatrix, als auch für die Mittelwerte der Variablen berechnet.

11.2 Identifizieren kritischer Werte

Wenn man ein Modell spezifiziert und bei der Betrachtung der Teststatistiken bemerkt, dass das Modell laut den Testschätzern knapp verworfen werden muss, kann es sinnvol sein, zu schauen, ob es kritische Werte gibt, die, wenn man sie in die Syntax mitaufnimmt, den Modellfit verbessern. Dieses Vorgehen kann sinnvoll sein, birgt aber auch die Gefahr, möglichst viele kritische Werte mit in die Syntax aufzunehmen, so dass letztendlich nicht mehr von einer Testung eines bestimmten Modells gesprochen werden kann. Aus diesem Grund sollte man sparsam damit umgehen, kritische Werte in die Syntax aufzunehmen. An einigen Stellen kann dies dennoch sinnvoll sein. Die Modification Indices geben an, in wie fern sich die $\chi$^2-Teststatistik verbessern würde, wenn ein bestimmter Parameter nicht eingeschränkt wäre. Auf dieser Grundlage wird die erwartete Parameterveränderung (“Expected Parameter Change”) berechnet, also der Wert, den der Parameter hätte, wenn er als freier Parameter in das Modell mitaufgenommen werden würde.

Um sich die einflussreichen Werte darstellen zu lassen, müssen keine weiteren Berechnungen vorgenommen werden. Aber auch hier ist es Voraussetzung, dass in lavaanGUI bereits Daten eingelesen und ein Modell spezifiziert wurde.

Die einflussreichen Daten werden, wie in Kapitel 5.5 bereits angesprochen, unter dem Menüpunkt “Modification Indices” des Hauptmenüs dargestellt. Für das bereits unter Kapitel 11.1 verwendete Beispiel des $\tau$-parallelen Modells, wurden folgende kritische Werte identifiziert:

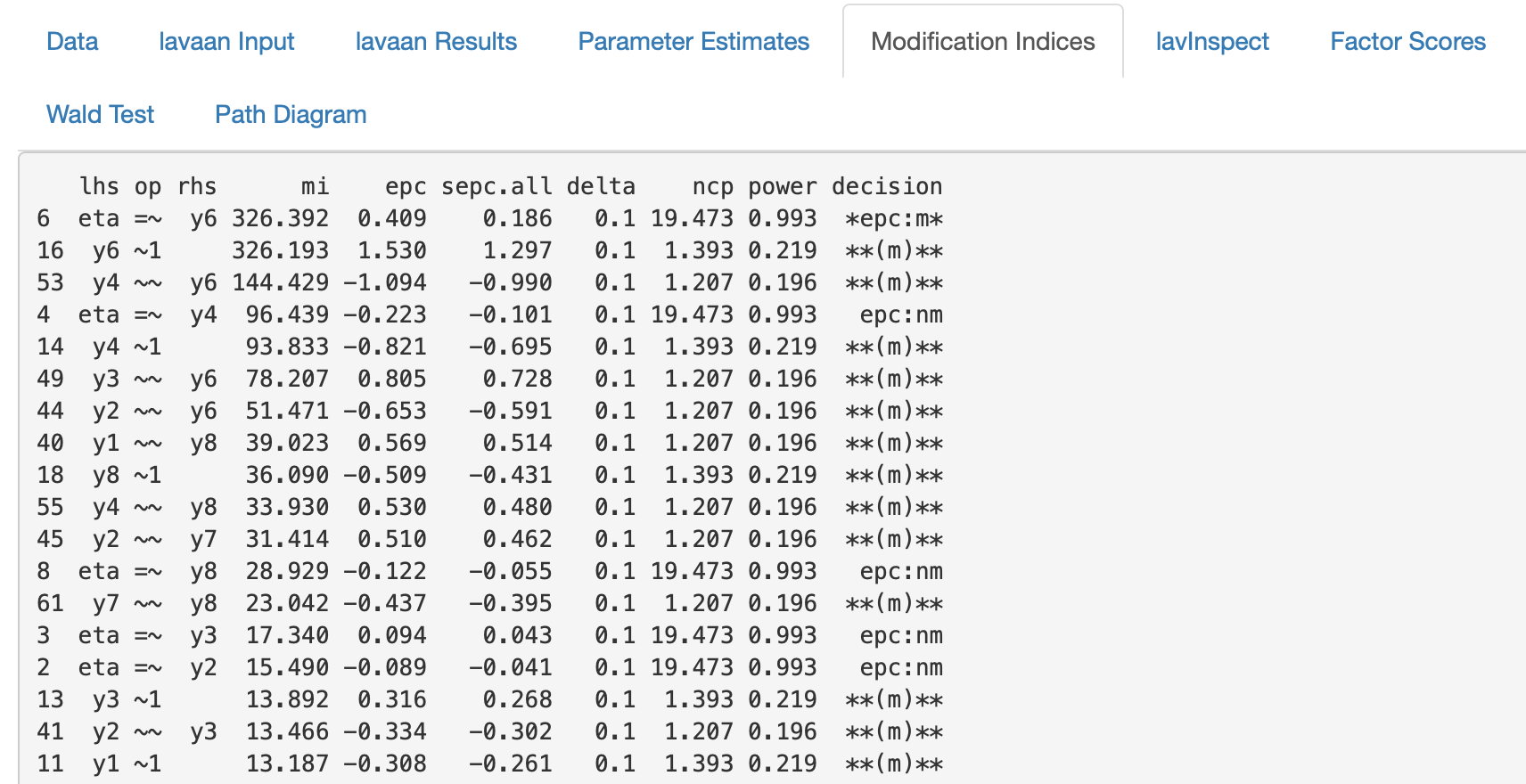
Figure 11.7: Modification Indices - Kritische Werte identifizieren

Die Spalten, die dabei am interessantesten für die Analyse und Identifikation der kritischen Werte sind, sind die Spalten “lhs”, “op”, “rhs”, “mi” und “epc”. Die Spalten “lhs”, “op” und “rhs” definieren die Parameter. In der Spalte “op” werden die mathematischen Operatoren angezeigt, die den Zusammenhang der zwei Parameter der Spalten “lhs” und “rhs” darstellen. Der Operator “=~” bezeichnet eine Faktorladung, der Operator “~~” Varianzen oder Kovarianzen und der Operator “~1” ein Intercept. In der Spalte “mi” wird der Modifikationsindex dargestellt. Dazugehörig wird in der Spalte “epc” die erwartete Parameterveränderung dargestellt. Je höher der “mi”-Wert eines Parameters ist, desto größer ist sein Einfluss auf die Spezifikation des Modells.

Gibt es sehr viele Modifikationsindices, die hohe Werte in der “mi”-Spalte aufweisen, sollte man das spezifizierte Modell nocheinmal überprüfen und gegebenenfalls ein weniger restriktives Modell spezifizieren und testen, um zu schauen, ob dieses besser an die Daten fitten würde.

Nachdem kritische Werte identifziert wurden, können diese in die Syntax mitaufgenommen werden. Dazu reicht es aus, wenn man die Parameter einer Zeile unter den Spalten “lhs”, “op” und “rhs” kopiert und in die Syntax mitaufnimmt.

Quelle: https://www.jstatsoft.org/article/view/v048i02/v48i02.pdf